При работе с растровыми основами в геоинформатике возникают вопросы их привязки к географическим проекциям. Исходное изображение, при этом, получают либо сканированием ранее отпечатанной карты, либо как цифровую фотографию поверхности земли. В обоих случаях изображение уже несет в себе нелинейные искажения, влияющие на дальнейшую привязку.

Так, сканированное изображение несет в себе искажения:

- устройства печати,

- устройства сканирования,

- из-за поворота листа при сканировании.

Фотографическое изображение содержит искажения от:

- неперпендикулярности направления фотографической камеры относительно поверхности,

- кривизны поверхности Земли,

- оптической системы объектива,

- рефракции атмосферы.

Борьба с искажениями может осуществляться как на этапе подготовки растрового изображения, так и при его последующем использовании. При этом в подготовку включается этап коррекции изображения по тестовым примерам, позволяющим оценить нелинейные искажения как отдельного устройства (нелинейность сканера), так и их комплекса (нелинейность объектива и ПЗС матрицы фотокамеры). Часто изображения поступают из внешнего источника в уже готовом виде и нет возможности произвести оценку внесенных в них искажений из-за недоступности оборудования поставщика. В обоих случаях функция, описывающая нелинейные искажения либо отсутствует, либо не является аналитической.

Как для коррекции изображений, так и для привязки растров к географической проекции используются два набора точек. Первый набор располагают на исходном растровом изображении, второй – на той основе, на которую изображение надо привести. Основой могут быть как регулярные сетки для коррекции сканера и другого оборудования, так и географические координаты в целевой проекции. При использовании регулярных сеток коррекции оборудования, точки на исходном изображении расставляют по результатам обработки той же регулярной сетки корректируемым оборудованием. В случаях привязки по географическим координатам исходными являются точки, координаты которых известны либо по нанесенной на растровое изображение географической сетке (сканированная карта), либо по характерным топологическим особенностям географического объекта (излом площадного объекта, характерный точечный объект).

Обработка наборов точек может происходить двумя разными способами: формированием одного полиномиального преобразования по методу наименьших квадратов, либо разбиением изображения на фрагменты, каждый из которых преобразуется по своему.

Аффинное преобразование по методу наименьших квадратов

Аффинное преобразование для всего изображения, удовлетворяющее условию наименьшей суммы квадратов ошибки.

Сетки преобразования

Сетки преобразования получаются из наборов точек привязки построением разбиения на фрагменты. При этом каждый фрагмент будет иметь привязку с фиксированной точностью, не влияющую на точность привязки других фрагментов изображения.

Сетка из треугольников

Самый простой вид сетки преобразования, получаемый триангуляцией наборов точек привязки. Самым оптимальной является равноугольная триангуляция (т.н. триангуляция Делоне).

Построение сетки

1. Построение сетки начинается с построения контура триангуляции. Контур должен быть выпуклым многоугольником, содержащим все точки привязки.

2. После построения контура, производится собственно построение сетки триангуляции путем последовательного добавления точек привязки в промежуточный результат триангуляции. Последовательность просмотра точек никак не влияет на результат триангуляции.

Обработка краев изображения

Точки привязки не всегда находятся на самых краях растрового изображения. Это приводит к тому, что область, охваченная триангуляционной сеткой, не содержит края изображения. Самым простым выходом из ситуации является отбрасывание неохваченных краев. Это приведет к необходимости учитывать последующее отбрасывание при размещении точек привязки, чтобы все интересующие нас фрагменты изображения были включены в сетку преобразования. Другой подход заключается в расширении сетки путем интерполяции точек привязки на края изображения.

Сетка из четырехугольников

Преобразования простых геометрических фигур

Теперь рассмотрим преобразование геометрических фигур, используемых для построения сеток.

Треугольник-треугольник

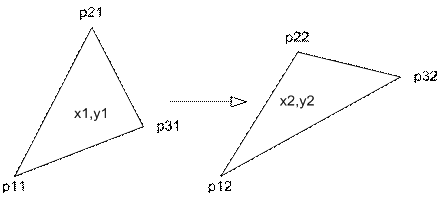
А. Получить (x1,y1) = f(x2,y2)

1. Введем обобщенные координаты u, v по сторонам 1-2 и 1-3 соответственно.

2. Тогда для x1, y1:

(1)

3. Аналогично (1) для x2, y2:

(2)

4. В матричном виде (1) и (2) выглядят так:

(3)

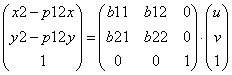(4)

где:

5. Разрешая (4) относительно u, v, получим:

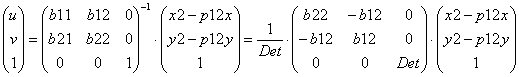(5)

где:

6. Подставляя (5) в (3) окончательно получим:

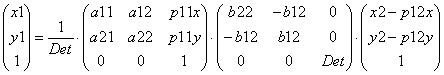(6)

или

(7)

Б. Получить границы сканирования x2, y2

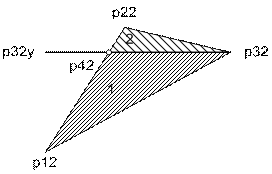
1. Произведем оконтуривание треугольника p12, p22, p32:

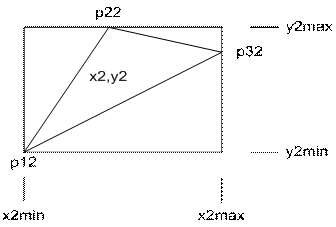
2. При этом получаем внешние границы изменения координат x2, y2:

(8)

3. Из прямоугольной области (8) получим треугольную, введя зависимость границ координаты x2 от y2. Для этого нам понадобится разделить треугольник на 2 части по y2:

1-я часть: от y2min до промежуточной точки,

2-я часть: от промежуточной точки до y2max

4. Для такого разбиения необходимо произвести линейное упорядочивание точек p12, p22, p32 по величине координаты y. В данном случае это: p12, p32, p22.

5. Переобозначим упорядоченные точки как: p2min, p2mid, p2max.

6. Согласно переобозначению в п.5 имеем 2 интервала для y2:

(9)

(10)

7. На интервале (8) имеем зависимость:

(11)

8. Аналогично на интервале (10) имеем:

(12)

9. Очевидно, что вторая граница имеет одинаковую зависимость как для 1-го, так и для второго интервалов, т.к. она скользит по одной и той же стороне тр-ка. Тогда:

(13)

10. Окончательно:

– сканирование по y2 разбивается на 2 интервала (9) и (10) в соответствии с пп. 4-6;

– сканирование по x2 имеет 2 плавающие границы:

– первая – по (11) и (12), соответственно;

– вторая – по (13)

При реализации алгоритма удобно рассчитывать границы по какому-либо алгоритму растеризации отрезка.

Четырехугольник-четырехугольник

А. Получить (x1,y1) = f(x2,y2)

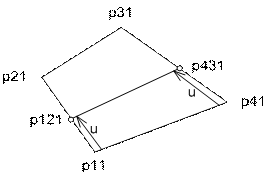
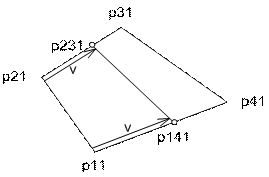
1. Введем обобщенные координаты u, v по сторонам 1-2 и 1-4 исходного четырехугольника. При этом область изменения каждой из координат – отрезок [0; 1]. Существует несколько способов отображения координат внутренней области четырехугольника на обобщенные координаты. Одни из них линейны, другие – нет. Для начала рассмотрим билинейное отображение.

Билинейное отображение

2. Произведем дополнительные построения для получения координат (x1, y1), соответствующих заданным (u, v).

	(1)
	(2)
	(3)

3. Подставив (1) и (2) в (3), получим:

(4)

объединяя множители, имеем:

(5)

4. В матричном виде (5) выглядит как:

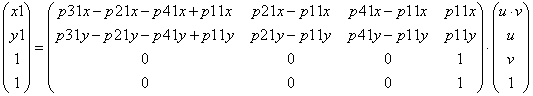(6)

5. Найдем обратное преобразование для (6). Для этого произведем замену коэффициентов:

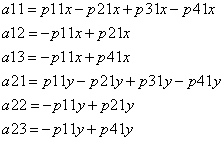, где: (7)

6. На основании (7) получим:

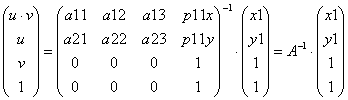
7. Очевидно, что матрица А – вырожденная и не имеет обратной. Поэтому, для получения (u, v) через (x2, y2) поступим другим образом: решим систему уравнений (5) относительно (u, v).

8. Аналогично (5), но для координат (x2, y2), получим билинейную систему уравнений:

(8)

где:

9. Выразим v через u согласно первому уравнению из системы уравнений (8):

(9)

10. Тогда, подставляя (9) во второе уравнение из системы уравнений (8), получим обыкновенное квадратное уравнение для u:

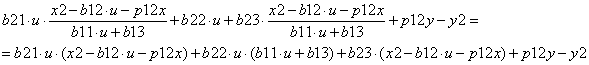
собрав сомножители, получим уравнение:

(10)

11. Соответственно, решая уравнение (10), получим:

(11)

где:

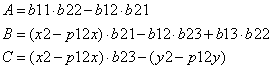
12. Т.к. область определения обобщенных координат – отрезок [0, 1], то (11) имеет только один вариант решения:

(12)

13. Полное преобразование находится в 2 этапа: (x2, y2)®(u, v) по формулам (9) и (12), а затем (u, v)®(x1, y1) по формуле (7). При этом обязательно надо учитывать ограничения, накладываемые уравнениями (9) и (12).

14. Помимо билинейного отображения четырехугольные области могут преобразовываться друг в друга перспективным отображением.

Перспективное отображение

15. В общем виде, перспективное отображение имеет вид [1] (стр. 431):

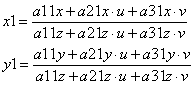(12)

где:

16. Имея 8 уравнений для 9 коэффициентов, примем и получим:

(13)

(14)

(15)

Подставив (14) и (15) в уравнения для и , получим систему уравнений:

(16)

17. Решая систему уравнений (16), получим:

(17)

где:

18. Подставляя результат (17) в (14) и (15) получим:

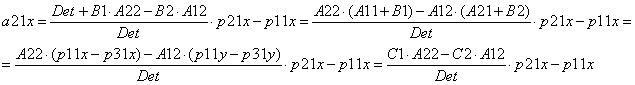
, где: (18)

аналогично

, где: (19)

19. Окончательно коэффициенты для перспективного отображения (12):

где:

20. Определив коэффициенты перспективного отображения (12), найдем обратное ему, составив систему уравнений, причем система координат (x1,y1) заменена на (x2,y2):

(20)

21. Решая систему уравнений (20), получаем:

(21)

где:

22. Полное преобразование находится в 2 этапа: (x2, y2)®(u, v) по формулам (21), а затем (u, v)®(x1, y1) по формулам (12). При этом коэффициенты в (x2, y2) для (21) находят аналогично коэффициентам для (x1, y1).

Б. Получить границы сканирования x2, y2

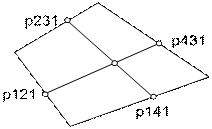
1. Произведем оконтуривание четырехугольника p12, p22, p32, p42:

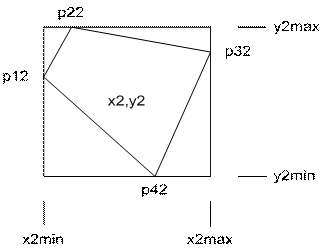
2. При этом получаем внешние границы изменения координат x2, y2:

(22)

3. …

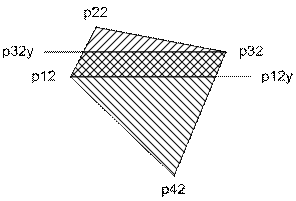
4. …

Литература и другие использованные источники информации

1. Шишкин Е.В. Боресков А.В. Компьютерная графика. Полигональные модели. – М.: ДИАЛОГ-МИФИ, 2001. – 464 с. ISBN 5-86404-139-4

2. http://algolist.manual.ru/maths/geom/deluanay.php

3. http://www.kgraph.narod.ru/lectures/lectures.htm

4. Майкл Ласло. Вычислительная геометрия и компьютерная графика на С++: Пер. с англ. – М.: «Бином», 1997. – 304 с.

5. Роджерс Д., Адаме Дж. Математические основы машинной графики: Пер. с англ. – М.: Мир, 2001. – 604 с.

6. Роджерс Д. Алгоритмические основы машинной графики: Пер. с англ. – М.: Мир, 1989. – 512 с.

7. http://thor-f5.er.usgs.gov/topomaps/rgc_urisa_1999.pdf